* 티스토리에서 마크다운 적용이 안돼서 깨지는 부분이 많습니다.
* 깨지지 않은 파일로 자세히 보기 원하시는 분들은 아래 링크 참고해주세요!
파이썬 머신러닝 완벽 가이드 - 5. Classification(3) (예제 및 스태킹)
EDA 중, head, info, describe 사용이상치 발생 ⇒ 제일 많은 걸로 대체하는 방법론도 있음LGBMClassifier( . . . boost_from_average=False) : 레이블값 매우 불균형한 경우 False, if True ⇒ 재현률 및 R
velog.io

4. 실전 예시
A. Santander 예시
- EDA 중, head, info, describe 사용
- 이상치 발생 ⇒ 제일 많은 걸로 대체하는 방법론도 있음
B. 신용카드 사기 검출 예시
LGBMClassifier( . . . boost_from_average=False): 레이블값 매우 불균형한 경우 False, if True ⇒ 재현률 및 ROC-AUC 성능 매우 저하
( : 왜인지는 아직 모름)
- 언더 샘플링과 오버 샘플링의 이해 : 지도 학습시 극도로 불균형한 레이블 값 분포로 인한 문제점을, 적절한 학습 데이터를 확보로 해결 방법들
(주로 오버 샘플링 방식이 예측 성능상 더 유리한 경우가 많아 주로 사용됨)

- 언더 샘플링 : 많은 데이터 세트를 적은 데이터 세트 수준으로 감소시키는 방식 ⇒ 너무 많은 정상 레이블 데이터를 감소시켜서, 오히려 학습이 잘 안될 수 있음
- 오버 샘플링 : 적은 데이터 세트를 많은 데이터 세트 수준으로 증식시키는 방식 ⇒ 동일한 데이터를 단순 증식하는 건 과적합 되기에 의미 X ⇒ 원본 피처 값들을 아주 약간만 변경하여 증식함
1. 대표적으로 SMOTE(Synthetic Minority Over-sampling Technique) 방법이 있음
2. SMOTE는 적은 제이터 세트에 있는 개별 데이터들의 K 최근접 이웃을 찾아서 이 데이터와 K개 이웃들의 차이를 일정 값으로 만들어거 기존 데이터와 약간 차이가 나는 새로운 데이터들을 생성하는 방식
3. SMOTE를 구현하는 파이썬 패키지 == imbalanced-learn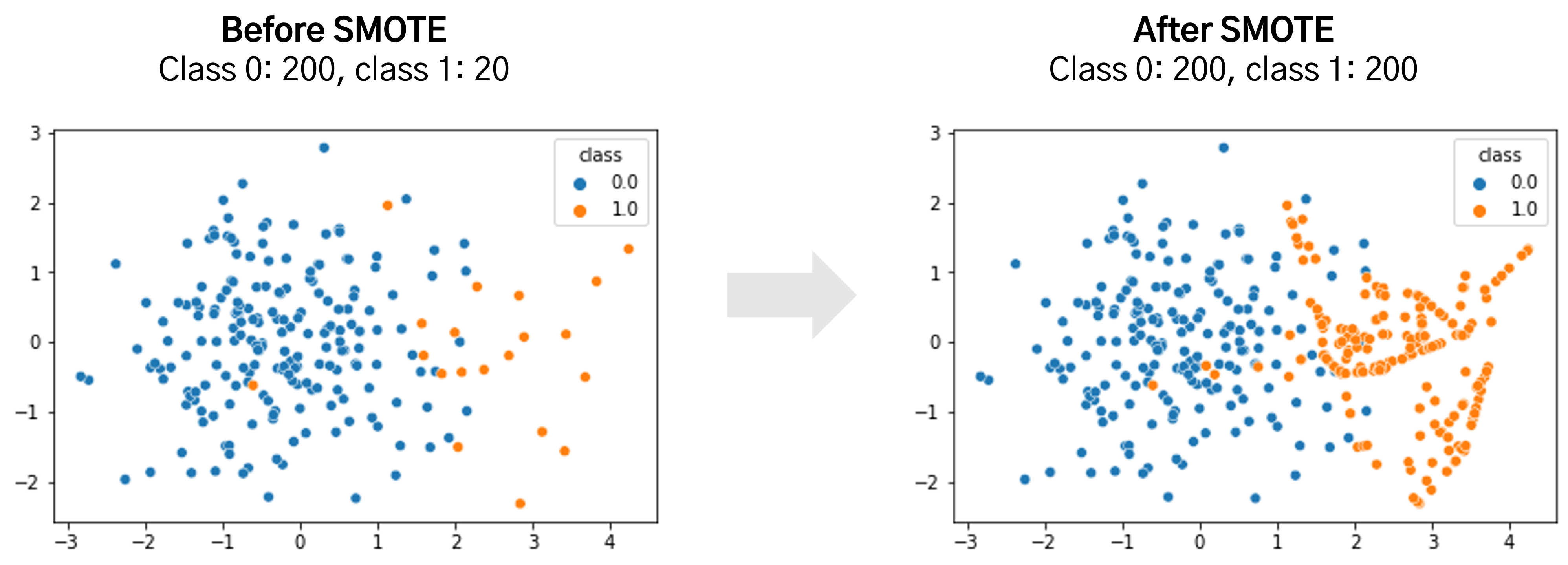
- (전처리) 데이터 분포도 변환
- StandardScaler : 로지스틱 회귀 같은 선형 회귀 경우, 중요 피처값들이 정규분포 유지하는 것을 선호함.
- 중요한 피처인 Amount를 sns.distplot 해보니 긴 꼬리 형태 ⇒ 정규분포형태로 전처리 (StandarScaler)
- 별로 큰 효과는 없었음
- StandardScaler : 로지스틱 회귀 같은 선형 회귀 경우, 중요 피처값들이 정규분포 유지하는 것을 선호함.
from sklearn.preprocessing import StandardScaler
# 사이킷런의 StandardScaler를 이용하여 정규분포 형태로 Amount 피처값 변환하는 로직으로 수정.
def get_preprocessed_df(df=None):
df_copy = df.copy()
scaler = StandardScaler()
print(df_copy['Amount'].values)
amount_n = scaler.fit_transform(df_copy['Amount'].values.reshape(-1, 1))
# 변환된 Amount를 Amount_Scaled로 피처명 변경후 DataFrame맨 앞 컬럼으로 입력
df_copy.insert(0, 'Amount_Scaled', amount_n)
# 기존 Time, Amount 피처 삭제
df_copy.drop(['Time','Amount'], axis=1, inplace=True)
return df_copy- 로그 변환 : 데이터 분포도가 심하게 왜곡돼있을 때 사용하면 좋음
- 원래 값을 log 값으로 변환해, 원래 큰 값을 상대적으로 작은 값으로 변환해주기에 데이터 분포도의 왜곡을 상당 수준 개선해 줌
- 약간식 개선됨
def get_preprocessed_df(df=None):
df_copy = df.copy()
# 넘파이의 log1p( )를 이용하여 Amount를 로그 변환
amount_n = np.log1p(df_copy['Amount'])
df_copy.insert(0, 'Amount_Scaled', amount_n)
df_copy.drop(['Time','Amount'], axis=1, inplace=True)
return df_copy- (전처리) 이상치 데이터 제거
- IQR (Inter Quantile Range) : 사분위 값의 편차를 이용하는 기법 → Q1(25%) ~ Q3(75%) 범위를 IQR이라고 부름 (중앙값에서 퍼져나간 정도)
⇒ IQR = Q3 - Q1
⇒ Box Plot으로 시각화 - IQR 이용해 이상치 데이터 검출하는 방식 : IQR * 1.5 하여 생성된 범위를 이용해, 최댓/최솟값을 결정한 뒤, 여기를 벗어나는 데이터를 이상치로 간주 ⇒ 경우에 따라 1.5가 변경될 수 있음
⇒ Q3(3/4분위수)에, IQR_1.5를 더함 == 최댓값
⇒ Q2(1/2분위수) == 중앙값
⇒ Q1(1/4분위수)에, IQR_1.5를 뻄 == 최솟값
- IQR (Inter Quantile Range) : 사분위 값의 편차를 이용하는 기법 → Q1(25%) ~ Q3(75%) 범위를 IQR이라고 부름 (중앙값에서 퍼져나간 정도)
from sklearn.preprocessing import StandardScaler
# 사이킷런의 StandardScaler를 이용하여 정규분포 형태로 Amount 피처값 변환하는 로직으로 수정.
def get_preprocessed_df(df=None):
df_copy = df.copy()
scaler = StandardScaler()
print(df_copy['Amount'].values)
amount_n = scaler.fit_transform(df_copy['Amount'].values.reshape(-1, 1))
# 변환된 Amount를 Amount_Scaled로 피처명 변경후 DataFrame맨 앞 컬럼으로 입력
df_copy.insert(0, 'Amount_Scaled', amount_n)
# 기존 Time, Amount 피처 삭제
df_copy.drop(['Time','Amount'], axis=1, inplace=True)
return df_copy
- 매우 많은 피처가 있을 경우, 이들 중 결정값(레이블)과 가장 상관성이 높은 피처 위주로 이상치를 검출해야 시간/성능에 유리함
import seaborn as sns
plt.figure(figsize=(9, 9))
corr = card_df.corr()
sns.heatmap(corr, cmap='RdBu')- IQR을 이용해, 이상치를 검출하는 함수 생성 ⇒ IQR 계산 ⇒ 최댓/최솟값 아웃라이어 찾기
import numpy as np
def get_outlier(df=None, column=None, weight=1.5):
# fraud에 해당하는 column 데이터만 추출, 1/4 분위와 3/4 분위 지점을 np.percentile로 구함.
fraud = df[df['Class']==1][column] # column = 'V14'
quantile_25 = np.percentile(fraud.values, 25)
quantile_75 = np.percentile(fraud.values, 75)
# IQR을 구하고, IQR에 1.5를 곱하여 최대값과 최소값 지점 구함.
iqr = quantile_75 - quantile_25
iqr_weight = iqr * weight
lowest_val = quantile_25 - iqr_weight
highest_val = quantile_75 + iqr_weight
# 최대값 보다 크거나, 최소값 보다 작은 값을 아웃라이어로 설정하고 DataFrame index 반환.
outlier_index = fraud[(fraud < lowest_val) | (fraud > highest_val)].index
return outlier_index
outlier_index = get_outlier(df=card_df, column='V14', weight=1.5)
print('이상치 데이터 인덱스:', outlier_index)- (전처리) SMOTE 오버 샘플링 적용
- SMOTE 적용시에는 반드시 train(학습) 데이터 세트만 오버 샘플링 해야함 → eval(검증), test(테스트) 데이터 세트 하면 올바른 검증/테스트 불가
from imblearn.over_sampling import SMOTE
smote = SMOTE(random_state=0)
X_train_over, y_train_over = smote.fit_resample(X_train, y_train) #fit_sample 없어지고 -> fit_resample로 바뀜
print('SMOTE 적용 전 학습용 피처/레이블 데이터 세트: ', X_train.shape, y_train.shape)
print('SMOTE 적용 후 학습용 피처/레이블 데이터 세트: ', X_train_over.shape, y_train_over.shape)
print('SMOTE 적용 후 레이블 값 분포: \n', pd.Series(y_train_over).value_counts())
lr_clf = LogisticRegression()
# ftr_train과 tgt_train 인자값이 SMOTE 증식된 X_train_over와 y_train_over로 변경됨에 유의
get_model_train_eval(lr_clf, ftr_train=X_train_over, ftr_test=X_test, tgt_train=y_train_over, tgt_test=y_test)- 재현율/AUC는 엄청 올라가지만, 정밀도, 정밀도/F1은 급격히 내려감 ⇒ 실무에 적용할 수 없음
- 실제 원본 데이터의 유형보다 너무나 많은 Class=1 데이터가 학습되어, 테스트 데이터 세트 예측에서 Class=1 예측이 너무 많아짐
precision_recall_curve_plot()으로 확인해보자 (추후 threshold를 변경하려나…?)- 실제로 그려보니, 임계값이 0.99이하에서는 재현율이 매우 좋고/정밀도가 극단적으로 낮다가, 0.99에는 급격히 서로 cross 됨
- 이건, threshold 바꿔도 성능을 얻을 수 없으므로, 이번 사례에서 로지스틱 회귀의 경우에는 SMOTE 적용하면 안된다는 결론
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
from sklearn.metrics import precision_recall_curve
%matplotlib inline
def precision_recall_curve_plot(y_test , pred_proba_c1):
# threshold ndarray와 이 threshold에 따른 정밀도, 재현율 ndarray 추출.
precisions, recalls, thresholds = precision_recall_curve( y_test, pred_proba_c1)
# X축을 threshold값으로, Y축은 정밀도, 재현율 값으로 각각 Plot 수행. 정밀도는 점선으로 표시
plt.figure(figsize=(8,6))
threshold_boundary = thresholds.shape[0]
plt.plot(thresholds, precisions[0:threshold_boundary], linestyle='--', label='precision')
plt.plot(thresholds, recalls[0:threshold_boundary],label='recall')
# threshold 값 X 축의 Scale을 0.1 단위로 변경
start, end = plt.xlim()
plt.xticks(np.round(np.arange(start, end, 0.1),2))
# x축, y축 label과 legend, 그리고 grid 설정
plt.xlabel('Threshold value'); plt.ylabel('Precision and Recall value')
plt.legend(); plt.grid()
plt.show()
precision_recall_curve_plot( y_test, lr_clf.predict_proba(X_test)[:, 1] )- LightGBM의 경우에는 SMOTE 활용하면, 이상치만 제거한 것에 비해 재현율은 높아지나, 정밀도는 낮아짐
- 일반적으로 SMOTE를 쓰면 재현율은 높아지나, 정밀도는 낮아짐
5. 스태킹 Stacking
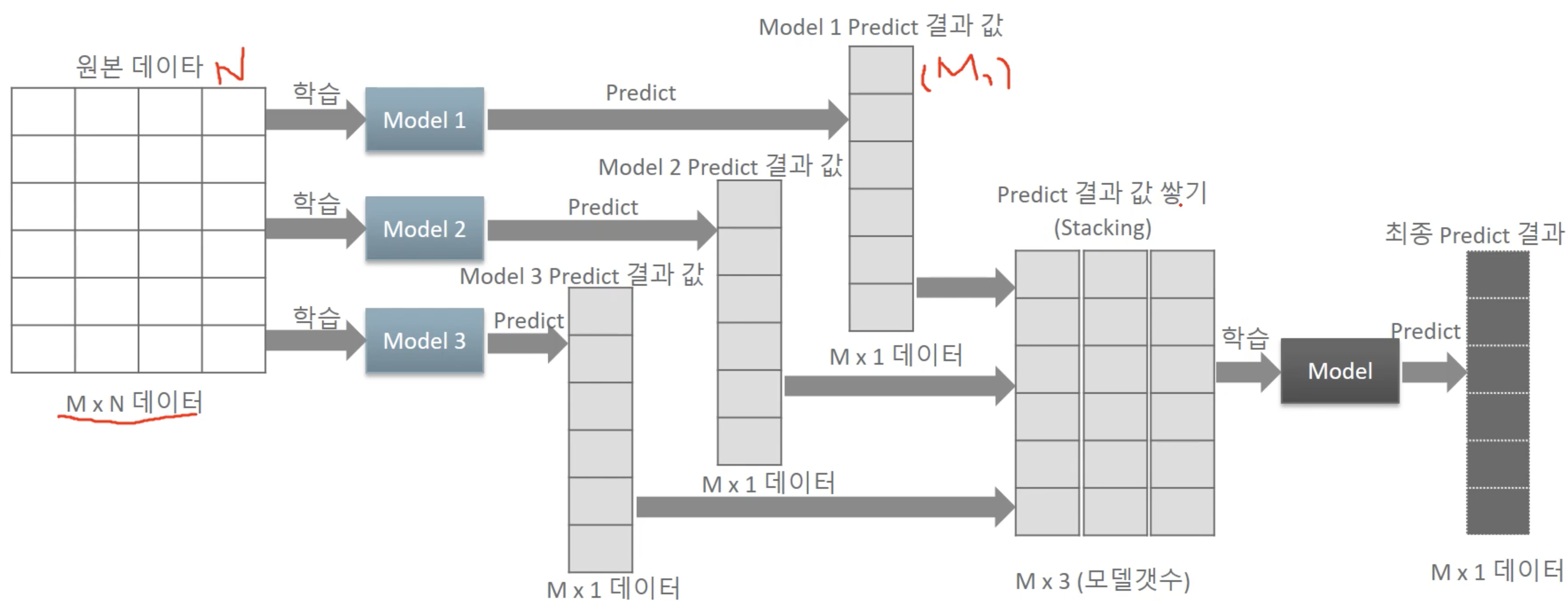
- 스태킹 앙상블 : 개별 알고리즘의 예측 결과 데이터 세트를 “최종적인 메타 데이터 세트”로 만들어 별도의 ML 알고리즘으로 최종학습을 수행하고 테스트 데이터를 기반으로 다시 최종 예측을 수행하는 방식
- 메타 모델: 개별 모델의 예측된 데이터 세트를 다시 기반으로 하여 학습하고 예측하는 방식
- 필요한 모델
- 개별적인 기반 모델
- 개별 기반 모델의 예측 데이터를 학습 데이터로 만들어서 학습하는 “최종 메타 모델”
# 개별 모델들을 학습/예측
knn_pred = knn_clf.predict(X_test)
rf_pred = rf_clf.predict(X_test)
dt_pred = dt_clf.predict(X_test)
ada_pred = ada_clf.predict(X_test)
pred = np.array([knn_pred, rf_pred, dt_pred, ada_pred])
print(pred.shape)
# transpose를 이용해 행과 열의 위치 교환. 컬럼 레벨로 각 알고리즘의 예측 결과를 피처로 만듦.
pred = np.transpose(pred)
print(pred.shape)
lr_final.fit(pred, y_test)
final = lr_final.predict(pred)
print('최종 메타 모델의 예측 정확도: {0:.4f}'.format(accuracy_score(y_test , final)))- CV 세트 기반의 스태킹 : 과적합 개선 위해, 최종 메타 모델을 위한 데이터 세트를 만들 때, 교차 검증 기반으로 예측된 결과 데이터 세트를 이용한다.
- 위 스태킹 코드에서, 로지스틱 회귀 메타모델 최종 학습시, 학습 데이터가 아닌 테스트용 데이터 기반으로 학습했기에 과적합이 발생할 수 있음
- 각 모델을 train data로 학습시킨 후
- 개별모델_pred = 개별모델.predict(X_test) ⇒ X_test 즉, 테스트용 데이터로 학습 시키고
- 최종 메타 모델때 y_test로 예측했으니 과적합 가능성 존재
- CV 세트 기반의 스태킹은 개별 모델들이, 각각 교차 검증으로,
[메타 모델을 위한 “학습용 스태킹 데이터 생성”] / [예측을 위한 “테스트용 스태킹 데이터”를 생성]한 뒤,
이를 기반으로 모델이 학습과 예측을 수행
⇒ 2단계의 스텝으로 구분 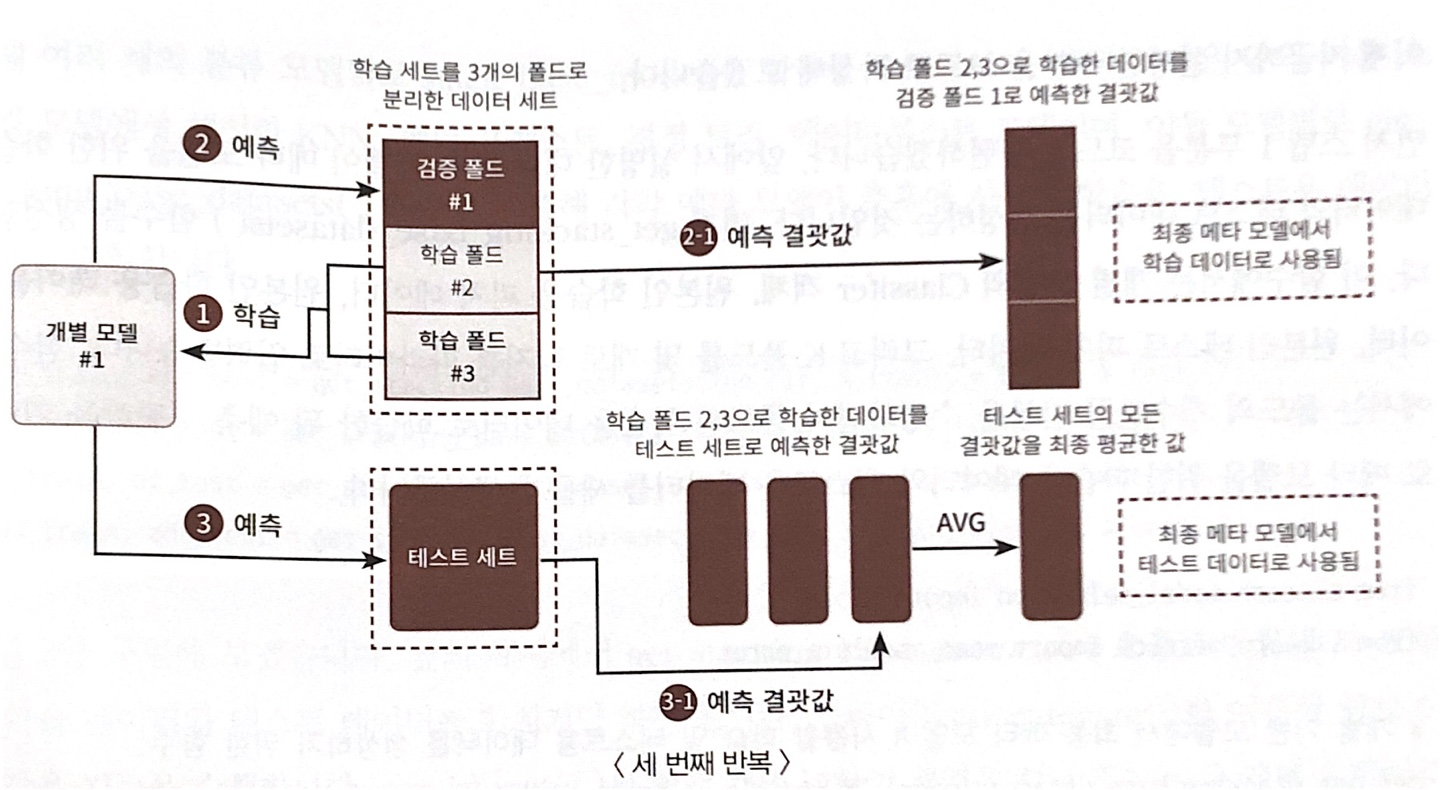
- 위 스태킹 코드에서, 로지스틱 회귀 메타모델 최종 학습시, 학습 데이터가 아닌 테스트용 데이터 기반으로 학습했기에 과적합이 발생할 수 있음
- CV 기반의 스태킹 모델 Step
- 각 모델 별로 원본 학습/테스트 데이터를 예측한 결과 값을 기반으로 메타 모델을 위한 학습/테스트용 데이터 생성
- 원본 학습 데이터 n(폴드)-1개로 학습된 개별 모델을 만듦
- 개별 모델로 원본 학습 데이터 폴드 1개를 Val 예측으로 [메타 학습 데이터] 칸 순차적으로 채우기
- 개별 모델로 원본 테스트 데이터 예측해서 결괏값 순차적으로 나열(?)하기
- 위 3개의 작업을 cv=n, n번 반복하면 ⇒ [메타 학습 데이터] 완성
- 그리고 n개의 원본 테스트 데이터에 대한 결괏값에 대한 AVG 구해서 [메타 테스트 데이터] 만들기
- [메타 학습/테스트 데이터] 완성 됐으니 그 다음부턴 그냥 fit, predict하면 됨
- 각 모델 별로 원본 학습/테스트 데이터를 예측한 결과 값을 기반으로 메타 모델을 위한 학습/테스트용 데이터 생성
# Step 1
from sklearn.model_selection import KFold
from sklearn.metrics import mean_absolute_error
# 개별 기반 모델에서 최종 메타 모델이 사용할 학습 및 테스트용 데이터를 생성하기 위한 함수.
def get_stacking_base_datasets(model, X_train_n, y_train_n, X_test_n, n_folds ):
# 지정된 n_folds값으로 KFold 생성.
kf = KFold(n_splits=n_folds, shuffle=False) #, random_state=0)
#추후에 메타 모델이 사용할 학습 데이터 반환을 위한 넘파이 배열 초기화
train_fold_pred = np.zeros((X_train_n.shape[0] ,1 ))
test_pred = np.zeros((X_test_n.shape[0],n_folds))
print(model.__class__.__name__ , ' model 시작 ')
for folder_counter , (train_index, valid_index) in enumerate(kf.split(X_train_n)):
#입력된 학습 데이터에서 기반 모델이 학습/예측할 폴드 데이터 셋 추출
print('\t 폴드 세트: ',folder_counter,' 시작 ')
X_tr = X_train_n[train_index]
y_tr = y_train_n[train_index]
X_te = X_train_n[valid_index]
#폴드 세트 내부에서 다시 만들어진 학습 데이터로 기반 모델의 학습 수행.
model.fit(X_tr , y_tr)
#폴드 세트 내부에서 다시 만들어진 검증 데이터로 기반 모델 예측 후 데이터 저장.
train_fold_pred[valid_index, :] = model.predict(X_te).reshape(-1,1)
#입력된 원본 테스트 데이터를 폴드 세트내 학습된 기반 모델에서 예측 후 데이터 저장.
test_pred[:, folder_counter] = model.predict(X_test_n)
# 폴드 세트 내에서 원본 테스트 데이터를 예측한 데이터를 평균하여 테스트 데이터로 생성
test_pred_mean = np.mean(test_pred, axis=1).reshape(-1,1)
#train_fold_pred는 최종 메타 모델이 사용하는 학습 데이터, test_pred_mean은 테스트 데이터
return train_fold_pred , test_pred_mean
knn_train, knn_test = get_stacking_base_datasets(knn_clf, X_train, y_train, X_test, 7)
rf_train, rf_test = get_stacking_base_datasets(rf_clf, X_train, y_train, X_test, 7)
dt_train, dt_test = get_stacking_base_datasets(dt_clf, X_train, y_train, X_test, 7)
ada_train, ada_test = get_stacking_base_datasets(ada_clf, X_train, y_train, X_test, 7)
# 각 모델별 학습/테스트 데이터 합치기
Stack_final_X_train = np.concatenate((knn_train, rf_train, dt_train, ada_train), axis=1)
Stack_final_X_test = np.concatenate((knn_test, rf_test, dt_test, ada_test), axis=1)
print('원본 학습 피처 데이터 Shape:',X_train.shape, '원본 테스트 피처 Shape:',X_test.shape)
print('스태킹 학습 피처 데이터 Shape:', Stack_final_X_train.shape,
'스태킹 테스트 피처 데이터 Shape:',Stack_final_X_test.shape)
# 최종 메타 모델 돌리기
lr_final.fit(Stack_final_X_train, y_train) # 최종 메타 모델 돌릴 때, 원본 학습 라벨 y_train 가져야 써야함
stack_final = lr_final.predict(Stack_final_X_test)
print('최종 메타 모델의 예측 정확도: {0:.4f}'.format(accuracy_score(y_test, stack_final)))정리
- 분류 Classification
- 결정 트리 Decision Tree
- Voting
- Bagging
- RandomForestClassifier
- Boosting
- GBM
- XGBoost
- LightGBM
- Stacking
'💻 파이썬 머신러닝 완벽 가이드' 카테고리의 다른 글
| 파이썬 머신러닝 완벽 가이드 - 6. Regression(2) (규제, 로지스틱회귀, 회귀 트리 및 예제) (0) | 2022.10.10 |
|---|---|
| 파이썬 머신러닝 완벽 가이드 - 6. Regression(1) (경사하강법, 평가지표, 선형회귀) (1) | 2022.10.05 |
| 파이썬 머신러닝 완벽 가이드 - 5. Classification(2) (앙상블) (0) | 2022.09.29 |
| 파이썬 머신러닝 완벽 가이드 - 5. Classification(1) (결정트리) (0) | 2022.09.29 |
| 파이썬 머신러닝 완벽 가이드 - 4. Evaluation (0) | 2022.09.28 |
