* 티스토리에서 마크다운 적용이 안돼서 깨지는 부분이 많습니다.
* 깨지지 않은 파일로 자세히 보기 원하시는 분들은 아래 링크 참고해주세요!
파이썬 머신러닝 완벽 가이드 - 6. Regression(1) (경사하강법, 평가지표, 선형회귀)
: 여러 개의 독립 변수와 한 개의 종속 변수 간의 상관관계를 모델링 하는 기법: 주어진 피처와 결정 값 데이터 기반에서 학습을 통해 최적의 회귀계수(Regression coefficients)를 찾아내는 것회귀계수
velog.io

Regression 회귀
: 여러 개의 독립 변수와 한 개의 종속 변수 간의 상관관계를 모델링 하는 기법
: 주어진 피처와 결정 값 데이터 기반에서 학습을 통해 최적의 회귀계수(Regression coefficients)를 찾아내는 것
- 회귀계수: 독립변수 값에 영향을 미치는 Wn
| 독립변수 갯수 | 회귀 계수의 결합 |
|---|---|
| 1개 : 단일 회귀 | 선형 : 선형 회귀 |
| 1개(n) ⁍ : 다항 회귀 | 선형 : 선형 회귀 |
| 여러개 : 다중 회귀 | 비선형 : 비선형 회귀 |
선형 회귀 : 실제 값과 예측 값의 차이(오류의 제곱 값)를 최소화하는 직선형 회귀선을 최적화하는 방식
- 일반 선형 회귀 : 실제-예측값의 RSS(Residual_잔여의_ Sum of Squares)를 최소화할 수 있도록 회귀 계수를 최적화하며, 규제를 적용하지 않은 모델
- 릿지 : 선형 회귀 + L2 규제 ⇒ L2 : 상대적으로 큰 회귀 계수 값의 예측 영향도를 감소시키기 위해 회귀 계수값을 더 작게 만드는 규제
- 라쏘 : 선형 회귀 + L1 규제 ⇒ L1 : (L2는 회귀계수값 크기 줄이는데 반해) 예측 영향력이 작은 피처의 회귀 계수를 0으로 만들어, 회귀예측시 피처가 선택되지 않게 하는 것 → L1 규제는 피처 선택 기능으로 불림
- 엘리스틱넷 : L2, L1 규제를 함께 결합한 모델 → 주로 피처가 많은 데이터 세트에 적용됨
- 로지스틱 회귀 : 분류에 사용되는 선형 회귀 모델
1. 경사하강법 Gradient Descent
- 단순 선형 회귀로 이해해보기
- 모델 : $f(x) = w_0 + w_1 * x$
- 실젯값 : $Y_i = w_0 + w_1 * X_i \cdots Error_i ; > ,$
- 예측값 : $\hat{Y} = w_0 + w_1*X$
- RSS(Residual Sum of Square) : 오류에 제곱을 해서 더하는 방식
- (오류값(잔차)은 +,- 모두 될 수 있기 때문에) 오류값의 제곱을 더한 방식
- $RSS(w_0,w_1) = 1/N\sum_{i=1}^{N}(y_i-(w_0+w_1x_i))^2$
- RSS에서는 독립변수 X, 종속변수 Y가 중심 변수가 아니라, 회귀 계수 w임을 인지하는 것이 매우 중요
- 학습 데이터로 입력되는 독립/종속변수는 RSS에서 모두 상수로 간주
- 회귀에서 이 RSS 값은 비용(Cost)이며, w변수(회귀계수) 구성되는 RSS를 비용 함수라고 함
- 회귀 알고리즘은 이 비용 함수가 반환하는 값(즉, 오류 값)을 지속해서 감소시키고 최종적으로는 더 이상 감소하지 않는 최소의 오류값을 구하는 것
- 비용 함수를 손실 함수(loss function)라고도 함
- 경사하강법: 점진적으로 반복적인 계산을 통해 W를 업데이트하면서 오류값이 최소가 되는 W를 구하는 방식
- 2차함수의 최저점은 미분 값인 1차 함수의 기울기가 가장 최소일 때
- $\begin{matrix}
R(w) &=& \frac{1}{N}\sum_{i=1}^N>(y_i->(w_0+w_1*x_i)>)^2 \ \
&=& \frac{1}{N}\sum_{i=1}^{N}>(y_i - \hat{y_i})^2 \ \ &=& 평균(>(실제값_i - 예측값_i)^2>) \ \ &=& 평균(오차제곱) \ \ &=& MSE
\end{matrix}$ - $R(w_0,w_1)$를 각 $w_0, w_1$로 편미분
- $\partial R(w)/\partial w_1 = \frac{2}{N} \sum_{i=1}^{N}-x_i * (y_i(-w_0+w_1x_i)) = -\frac{2}{N}\sum_{i=1}^{N}x_i*(실제값_i-예측값_i)$
- $\partial R(w)/\partial w_0 = \frac{2}{N} \sum_{i=1}^{N}-(y_i-(w_0+w_1x_i)) = -\frac{2}{N}\sum_{i=1}^{N}(실제값_i-예측값_i)$
-

- $w_1, w_0$의 편미분 결괏값인 $-\frac{2}{N}\sum_{i=1}^{N}x_i*(실제값i-예측값_i)$, $-\frac{2}{N}\sum{i=1}^{N}(실제값_i-예측값_i)$ 을 반복적으로 보정하면서, $w_1, w_0$ 값을 업데이트 하면서 비용 함수 $R(w)$를 최소가 되는 $w_0, w_1$ 을 구할 수 있음
- 이때, 편미분 값이 너무 클 수 있기 때문에 보정계수 $\eta$를 곱하는데, 이를 학습률(learning_rate)이라고 한다.
- 업데이트는 편미분 결괏값을 마이너스(-)하면서 적용
- $새로운;w_1 = 이전;w_1 - (>-\eta\frac{2}{N} \sum_{i=1}^{N}x_i(실제값_i-예측값_i)>)$
- $새로운;w_0 = 이전;w_0 - (>- \eta \frac{2}{N} \sum_{i=1}^{N} (실제값_i-예측값_i)>)$
- 이 과정을 반복적으로 적용하면서, 비용함수가 최소가 되는 값을 찾는 것
- 경사 하강법의 일반적인 프로세스
- [Step 1] : $w_1, w_0$을 임의의 값으로 설정하고 첫 비용 함수의 값을 계산
- [Step 2] : $w_1$을 $w_1 + \eta\frac{2}{N} \sum_{i=1}^{N}x_i(실제값i-예측값_i)$ 으로, $w_0$을 $w_0 + \eta \frac{2}{N} \sum{i=1}^{N} (실제값_i-예측값_i)$ 으로 업데이트한 후, 다시 비용 함수의 값을 계산
- [Step 3] : 비용 함수의 값이 감소했으면, 다시 [Step 2]를 반복, 더 이상 비용 함수 값이 감소하지 않으면 그때의 $w_1,w_0$를 구하고 반복 중지
```python
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
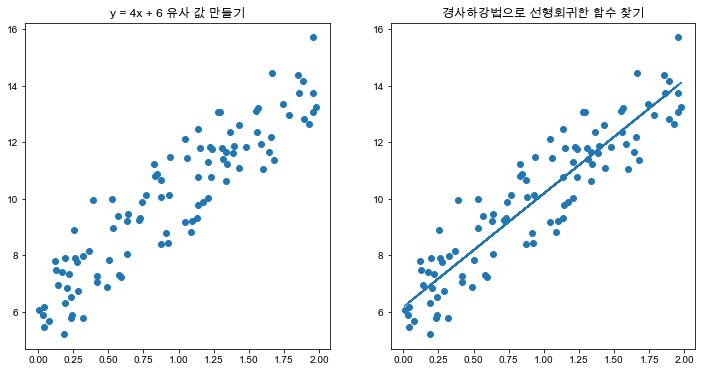
### --- 실제값을 Y=4X+6 시뮬레이션하는 데이터 값 생성 ----------------------------
np.random.seed(0)
# y = 4X + 6 식을 근사(w1=4, w0=6). random 값은 Noise를 위해 만듬
X = 2 * np.random.rand(100,1)
y = 6 +4 * X+ np.random.randn(100,1)
print(type(X))
### --- w0과 w1의 값을 최소화 할 수 있도록 업데이트 수행하는 함수 생성 ---------------------
# w1 과 w0 를 업데이트 할 w1_update, w0_update를 반환.
def get_weight_updates(w1, w0, X, y, learning_rate=0.01):
N = len(y)
# 먼저 w1_update, w0_update를 각각 w1, w0의 shape와 동일한 크기를 가진 0 값으로 초기화
w1_update = np.zeros_like(w1)
w0_update = np.zeros_like(w0)
# 예측 배열 계산하고 예측과 실제 값의 차이 계산
y_pred = np.dot(X, w1.T) + w0 # 예측값
diff = y - y_pred # 실제값 - 예측값
# diff == error
# w0_update를 dot 행렬 연산으로 구하기 위해 모두 1값을 가진 행렬 생성
w0_factors = np.ones((N,1))
# w1과 w0을 업데이트할 w1_update와 w0_update 계산
w1_update = -(2/N)*learning_rate*(np.dot(X.T, diff)) # w1의 편미분 값
w0_update = -(2/N)*learning_rate*(np.dot(w0_factors.T, diff)) # w0의 편미분 값
return w1_update, w0_update
### --- 반복적으로 경사 하강법을 이용하여 get_weigth_updates()를 호출하여 w1과 w0를 업데이트 하는 함수 생성 ---
# 입력 인자 iters로 주어진 횟수만큼 반복적으로 w1과 w0를 업데이트 적용함.
def gradient_descent_steps(X, y, iters=10000):
# w0와 w1을 모두 0으로 초기화.
w0 = np.zeros((1,1))
w1 = np.zeros((1,1))
# 인자로 주어진 iters 만큼 반복적으로 get_weight_updates() 호출하여 w1, w0 업데이트 수행.
for ind in range(iters):
w1_update, w0_update = get_weight_updates(w1, w0, X, y, learning_rate=0.01) # w1, w0 편미분값 return
w1 = w1 - w1_update # 새로운 w1
w0 = w0 - w0_update # 새로운 w0
return w1, w0
### --- 예측 오차 비용을 계산을 수행하는 함수 생성 및 경사 하강법 수행 ---------------------
def get_cost(y, y_pred):
N = len(y)
cost = np.sum(np.square(y - y_pred))/N # 평균( (실제값 - 예측값)^2 ) = RMSE
return cost
w1, w0 = gradient_descent_steps(X, y, iters=1000)
print("w1:{0:.3f} w0:{1:.3f}".format(w1[0,0], w0[0,0]))
y_pred = w1[0,0] * X + w0
print('Gradient Descent Total Cost:{0:.4f}'.format(get_cost(y, y_pred)))
```
- 경사하강법은 모든 학습 데이터에 반복적으로 업데이트 하기에 시간이 매우 오래 걸린다는 단점 ⇒ 확률적 경사하강법을 대신 사용- (미니배치) 확률적 경사하강법(Stochastic_통계학의/확률적인_ Gradient Desent): 일부 데이터만을 이용해 w가 없데이트되는 값 계산 ⇒ SGD
- 전반적으로 경사하강법과 비슷하지만, 전체 X, y 데이터에서 랜덤하게 batch_size만큼 데이터를 추출해서 w1, w0을 업데이트 함
def stochastic_gradient_descent_steps(X, y, batch_size=10, iters=1000): w0 = np.zeros((1,1)) w1 = np.zeros((1,1)) prev_cost = 100000 iter_index =0 for ind in range(iters): np.random.seed(ind) # 전체 X, y 데이터에서 랜덤하게 batch_size만큼 데이터 추출하여 sample_X, sample_y로 저장 stochastic_random_index = np.random.permutation(X.shape[0]) # permutation : array를 복사해서 shuffle sample_X = X[stochastic_random_index[0:batch_size]] sample_y = y[stochastic_random_index[0:batch_size]] # 랜덤하게 batch_size만큼 추출된 데이터 기반으로 w1_update, w0_update 계산 후 업데이트 w1_update, w0_update = get_weight_updates(w1, w0, sample_X, sample_y, learning_rate=0.01) w1 = w1 - w1_update w0 = w0 - w0_update return w1, w0 w1, w0 = stochastic_gradient_descent_steps(X, y, iters=1000) print("w1:",round(w1[0,0],3),"w0:",round(w0[0,0],3)) y_pred = w1[0,0] * X + w0 print('Stochastic Gradient Descent Total Cost:{0:.4f}'.format(get_cost(y, y_pred)))
- 피처가 여러개인 경우 어떻게 회귀 계수 도출할 수 있을까? (↔ 지금까지는 피처 1개, 독립변수 1개인 단순 선형 회귀의 경사하강법)
- 피처 1개인 경우 : $\hat{Y} = w_0 + w_1 * X$ 로
- 피처가 M개($X_1, X_2, \cdots, X_m$) 인 경우 : $\hat{Y} = w_0 + w_1 * X_1 + w_2 * X_2 + \cdots + w_{100}*X_{100}$
- 회귀 계수도는 M+1개 (1개는 $w_0$)
- 데이터가 N개이고 피처가 M개인 입력 행렬을 $X_{mat}$, 회귀 계수 $w_1, w_1, \cdots, w_{100}$을 W 배열로 표기하면
⇒ $\hat{Y} = np.dot(X_{mat}, W^T) + w_0$ - $w_0$을 W배열에 포함시키기 위해서, $X_{mat}$의 맨 처음 열에 모든 데이터 값이 1인 피처 Feat 0을 추가 하면
⇒ $\hat{Y} = X_{mat} * W^T$
2. 회귀 평가지표
- 보스턴 주택 가격 예측 예시
- LinearRegression 클래스는 RSS를 최소화해 OLS(Ordinary Least Squares) 추정 방식으로 구현됨
fit()메서드로 X, y 배열 받으면, 회귀 계수(Coefficients)인 W를coef_속성에 저장- 입력 파라미터에서, $nomalize=True$ 로 설정하면 회귀 수행 전, 입력 데이터 세트를 정규화함 $*default = False$
- OLS 기반 회귀 계수 계산은 입력 피처의 독립성에 많은 영향을 받아, 피처 상관관계가 높은 경우 분산이 매우 커져 오류에 매우 민감해짐
- 다중회귀(비선형) ⇒ 다중 공선성 문제 (multi-collinearity)
- 그래서 일반적으로 상관 관계가 높은 피처가 많은 경우 독립적인 중요한 피처만 남기고 제거 or 규제 및 PCA로 차원 축소 수행하기도 함
- LinearRegression 클래스는 RSS를 최소화해 OLS(Ordinary Least Squares) 추정 방식으로 구현됨
- MAE(Mean Absolute Error)
- $1/N \sum_{i=1}^{N}|Y_i - \hat Y_i|$
- 실제값과 예측값의 차이를 절대값으로 변환해 평균한 것
- 사이킷런 평가지표:
metrics.mean_absolute_error - Scoring 함수 적용값 : ‘neg_mean_absolute_error’
- ‘neg_’ ⇒ -1을 곱해서 반환 (scoring함수는 값이 클수록 좋은 평가 결과로 보기 때문)
- 10 > 1 ⇒ -10 < -1 == neg_mean_absolute_error ⇒ -1 * metrics.mean_absolute_error
- MSE(Mean Squared Error)
- $MSE = 1/N\sum_{i=1}^{N}(Y_i-\hat Y_i)^2$
- 실제값과 예측값의 차이를 제곱해 평균한 것
metrics.mean_squared_error- Scoring 함수 적용값 : ‘neg_mean_squared_error’
- RMSE(Root MSE)
- $RMSE = \sqrt{1/N\sum_{i=1}^{N}(Y_i-\hat Y_i)^2}$
- MSE는 실제 오류 평균보다 커지므로 보정한 것
- 사이킷런은 RMSE를 제공하지 않음
- $R^2$
- $R^2 = \frac{예측분산}{실제분산}$
- $R^2 = 1 - \frac { \sum ( y - \hat{y} )^2 } { \sum ( y - 평균 )^2 } = 1 - \frac { \sum ( 오차 )^2 } { \sum ( 편차 )^2 }$
- 1에 가까워질 수록 예측 정확도가 좋은 것
- $R^2 = 1 = (>1 - \color{yellow}0\color{d}>)$ ⇒ $\frac { \color{yellow}\sum ( 오차 )^2 } { \sum ( 편차 )^2 } = \frac {\color{yellow} \sum ( y - \hat{y} )^2 } { \sum ( y - 평균 )^2 }$ ⇒ $\color{yellow}{(y - \hat{y}) = 0}$ ⇒ $\color{yellow} y = \hat{y}$ ⇒ 예측값이 실제값과 같다
- $R^2 = 0 = (>1 - \color{red}1\color{d}>)$ ⇒ $\frac { \color{red}\sum ( 오차 )^2 } { \color{red} \sum ( 편차 )^2 } = \frac {\color{red} \sum ( y - \hat{y} )^2 } {\color{red} \sum ( y - 평균 )^2 }$ ⇒ $\color{red}{(y - \hat{y}) = (y - 평균)}$ ⇒ $\color{red} 평균 = \hat{y}$ ⇒ 예측값이 평균값과 같다 (예측하나마나다)
metrics.r2_score- Scoring 함수 적용값 : ‘r2’
3. 선형 회귀 Linear Regression
: 예측값과 실제값의 RSS를 최소화해 OLS(Ordinary Least Squares) 추정방식으로 구현한 클래스
- 입력 파라미터
| 파라미터 | 디폴트 | 설명 |
| --- | --- | --- |
| fit_intercept | Ture | Boolean, intercept(절편)값을 계산할 것인지 결정 |
| normalize | False | Boolean, True면 회귀를 수행하기 전에 입력 데이터 세트 정규화, fit_intercept=False 인 경우 이 파라미터는 무시됨 |- 속성
- coef_: fit() 메서드를 수행했을 때, 회귀 계수가 배열 형태로 저장되는 속성, shape = (Target 개수, 피처 개수)
- intercept_: 절편 값
- Seaborn의 regplot(): x, y축 값의 산점도와 선형 회귀 직선을 그려준다.
4. 다항 회귀 Polynomial Regression
: 회귀가 독립변수의 단항식이 아닌 2차, 3차 방정식과 같은 다항식으로 표현되는 것(하지만 선형회귀다!)
예) $y = w_0 + w_1x_1 + w_2x_2 + w_3x_1x_2 + w_4x_1^2 + w_5x_2^2$
- 선형회귀 / 비선형 회귀를 나누는 기준 : 회귀 계수가 선형/비선형인지에 따른 것(독립변수의 선형/비선형은 X)
- 사이킷런은 다항회귀를 위한 클래스를 명시적으로 제공 X
from sklearn.preprocessing import PolynomialFeatures
import numpy as np
# 다항식으로 변환한 단항식 생성, [[0,1],[2,3]]의 2X2 행렬 생성
X = np.arange(4).reshape(2,2)
print('일차 단항식 계수 feature:\n',X )
# degree = 2 인 2차 다항식으로 변환하기 위해 PolynomialFeatures를 이용하여 변환
poly = PolynomialFeatures(degree=2) # 2차 다항값을 만들겠다는 것
poly.fit(X)
poly_ftr = poly.transform(X)
print('변환된 2차 다항식 계수 feature:\n', poly_ftr)
------------------------------------------
> 일차 단항식 계수 feature:
> [[0 1]
> [2 3]]
> 변환된 2차 다항식 계수 feature:
> [[1. 0. 1. 0. 0. 1.]
> [1. 2. 3. 4. 6. 9.]]- 3차 다항식 계수의 피처값과 3차 다항식 결정값으로 학습
# 3 차 다항식 변환
poly_ftr = PolynomialFeatures(degree=3).fit_transform(X)
print('3차 다항식 계수 feature: \n',poly_ftr)
# Linear Regression에 3차 다항식 계수 feature와 3차 다항식 결정값으로 학습 후 회귀 계수 확인
model = LinearRegression()
model.fit(poly_ftr,y)
print('Polynomial 회귀 계수\n' , np.round(model.coef_, 2))
print('Polynomial 회귀 Shape :', model.coef_.shape)
------------------------------------------------
> 3차 다항식 계수 feature:
> [[ 1. 0. 1. 0. 0. 1. 0. 0. 0. 1.]
> [ 1. 2. 3. 4. 6. 9. 8. 12. 18. 27.]]
> Polynomial 회귀 계수
> [0. 0.18 0.18 0.36 0.54 0.72 0.72 1.08 1.62 2.34]
> Polynomial 회귀 Shape : (10,)- Polynomial Features로 변환 후 LinearRegression 사용 (Pipeline) (fit_transform 없이)
from sklearn.pipeline import Pipeline
def polynomial_func(X):
y = 1 + 2*X[:,0] + 3*X[:,0]**2 + 4*X[:,1]**3
return y
# Pipeline 객체로 Streamline 하게 Polynomial Feature변환과 Linear Regression을 연결
model = Pipeline([('poly', PolynomialFeatures(degree=3)),
('linear', LinearRegression())])
X = np.arange(4).reshape(2,2)
y = polynomial_func(X)
model = model.fit(X, y)
print('Polynomial 회귀 계수\n', np.round(model.named_steps['linear'].coef_, 2))
------------------------------------------------
> Polynomial 회귀 계수
> [0. 0.18 0.18 0.36 0.54 0.72 0.72 1.08 1.62 2.34]- 차수가 높아질 수록 과적합의 문제가 발생한다.
- 편향-분산 트레이드 오프(Bias-Variance Trade off)
- 고편향: 매우 단순화된 모델
- 고분산: 매우 복잡한 모델, 지나치게 높은 변동성
- 최적 모델을 위한 비용함수 구성요소: 학습 데이터 잔차 오류 최소화 + 회귀 계수 크기 제어
- alpha : 학습 데이터 적합정도와 회귀 계수 값의 크기 제어를 수행하는 튜닝 파라미터
- alpha를 크게하면 w를 작게, alpha를 작게하면 w이 어느정도 크게하여(커져도) 상쇄함 $for$ 과적합 개선
- ⇒ 비용함수 목표: $Min(RSS(w) + alphaX||w||_2^2)$
'💻 파이썬 머신러닝 완벽 가이드' 카테고리의 다른 글
| 파이썬 머신러닝 완벽 가이드 - 7. Dimension Reduction(1) (PCA, LDA) (1) | 2022.10.11 |
|---|---|
| 파이썬 머신러닝 완벽 가이드 - 6. Regression(2) (규제, 로지스틱회귀, 회귀 트리 및 예제) (0) | 2022.10.10 |
| 파이썬 머신러닝 완벽 가이드 - 5. Classification(3) (예제 및 스태킹) (0) | 2022.10.04 |
| 파이썬 머신러닝 완벽 가이드 - 5. Classification(2) (앙상블) (0) | 2022.09.29 |
| 파이썬 머신러닝 완벽 가이드 - 5. Classification(1) (결정트리) (0) | 2022.09.29 |
